用二次函数实现平滑的手势驱动动画

写这篇文章的动机来源于最近做的个动画，如上。其中我一开始在处理pan-to-dismiss的图片形变时候遇到了点问题。

首先，这个动画的思路是，以panGesture的transition.y为变量，去实时改变视图的CATransform3D属性。具体的，我们需要同时改变CATransform3DRotate和CATransform3DScale，这样才能在实现绕X轴转动的同时一起做缩放变换。而且，CATransform3DRotate这个属性需要从0增加到1，达到1后立即从1减小到0(因为视图向内旋转之后还需要再转回来)。除此之外，还需要判断transition.y的正负，因为我们需要当transition.y>0的时候，视图下半部分向屏幕内方向转（也就是CATransform3DRotate中x为-1），反之向屏幕外方向转。

OK，有了这个思路，我一开始就很直接地如下这么做了：

   #define SCROLLDISTANCE  200.0 //滑动的最大距离
   ...    

   CGFloat factorOfAngle = 0.0f;
   CGFloat Y = MIN(SCROLLDISTANCE,MAX(0,ABS(transition.y)));
   if(pan.state == UIGestureRecognizerStateChanged){

      factorOfAngle = Y<= SCROLLDISTANCE ? MIN(1,Y / SCROLLDISTANCE) : MAX(0, 1 - MAX(0, (Y - SCROLLDISTANCE) / SCROLLDISTANCE));
      CATransform3D t = CATransform3DIdentity;
      t.m34  = 1.0/-1000;
      t = CATransform3DRotate(t,factorOfAngle*(M_PI/5), transition.y>0?-1:1, 0, 0);
      currentPhoto.layer.transform = t;
   }

   ...

其中，factorOfAngle是一个控制在0~1的系数，并且从0增长到1,之后立即从1减小到0。

但是，效果很不好，动画显得很生硬。原因出在factorOfAngle的公式。仔细思考不难发现，factorOfAngle是关于transition.y的线性分段函数 ———— factorOfAngle = Y<= SCROLLDISTANCE ? MIN(1,Y / SCROLLDISTANCE) : MAX(0, 1 - MAX(0, (Y - SCROLLDISTANCE) / SCROLLDISTANCE))，且每段都是一个一次函数。以图表形式直观地看就是：

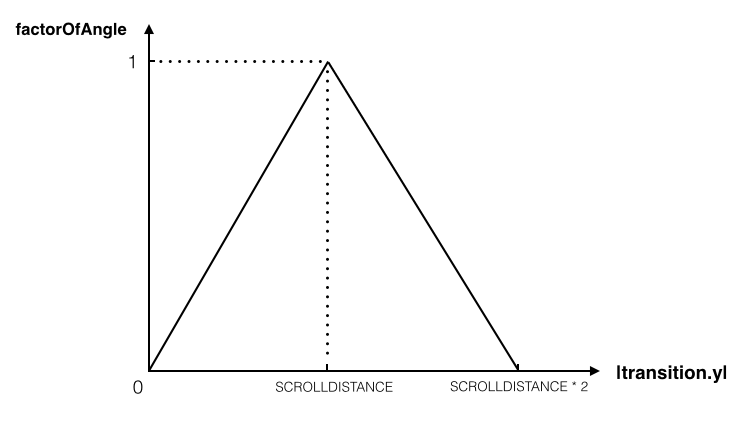
意识到这一点，下一步就很容易想到了，我们需要改变这条曲线，把它变成稍微平滑一点的曲线，比如我们可以改成下面这样：

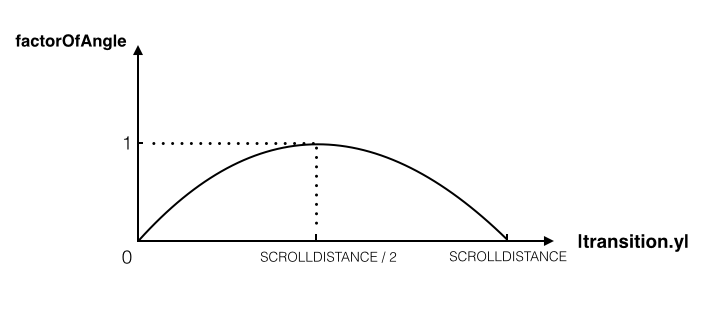
有没有觉得曲线很熟悉，是的，可以近似地看成一条一元二次曲线，变量为transition.y(准确的说，应该是ABS(transition.y),且0 <= ABS(transition.y) <= SCROLLDISTANCE )。建模完成，然后就是复习高中知识的时间了：

题目：已知一条开口向下的二次曲线，顶点为(SCROLLDISTANCE/2,1),且经过(0,0)和(SCROLLDISTANCE,0)两点，定义域为[0,SCROLLDISTANCE]，求该曲线的方程。

交点式、顶点式、基本式什么的...方法太多了，分分钟求出来如下：

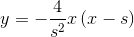
所以用代码表示出factorOfAngle的公式就是：

     CGFloat Y =MIN(SCROLLDISTANCE,MAX(0,ABS(transition.y)));
     factorOfAngle = MAX(0,-4/(SCROLLDISTANCE*SCROLLDISTANCE)*Y*(Y-SCROLLDISTANCE));

然后就是设置视图的CATransform3DRotate属性：

        CATransform3D t = CATransform3DIdentity;
        t.m34  = 1.0/-1000;
        t = CATransform3DRotate(t,factorOfAngle*(M_PI/5), transition.y>0?-1:1, 0, 0); //1

//1 最大绕X轴翻转角度为36°，也就是 M_PI/5

以上是关于视图的CATransform3DRotate属性的，但我们还需要实现视图的CATransform3DScale属性，同样的，先确定以什么样的平滑曲线进行动画，由于这时我们不需要像Rotate一样从0变到1再从1变到0，我们只需要让0平滑地变到1即可，因此，很快地就可以确定函数图像：

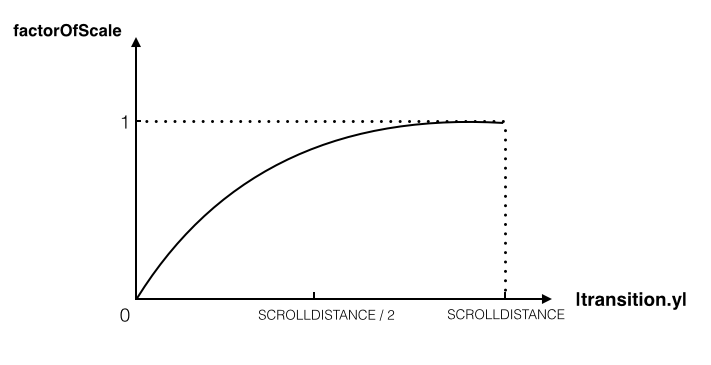
建模：

题目：已知一条开口向下的二次曲线，顶点为(SCROLLDISTANCE,1),且经过(0,0)和(2*SCROLLDISTANCE,0)两点，定义域为[0,SCROLLDISTANCE]，求该曲线的方程。

也是分分钟的事情：

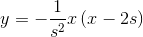
所以用代码表示出factorOfScale的公式就是：

    ...
    factorOfScale = MAX(0,-1/(SCROLLDISTANCE*SCROLLDISTANCE)*Y*(Y-2*SCROLLDISTANCE));
    ...
    t = CATransform3DScale(t, 1-factorOfScale*0.2, 1-factorOfScale*0.2, 0);

//1 当factorOfScale ＝＝ 1时，达到最大缩放状态，为原来的0.8倍（1-0.2）

综上所述，完成代码如下：

        CGFloat factorOfAngle = 0.0f;
        CGFloat factorOfScale = 0.0f;

        CGFloat Y =MIN(SCROLLDISTANCE,MAX(0,ABS(transition.y)));

        //一个开口向下,顶点(SCROLLDISTANCE/2,1),过(0,0),(SCROLLDISTANCE,0)的二次函数
        factorOfAngle = MAX(0,-4/(SCROLLDISTANCE*SCROLLDISTANCE)*Y*(Y-SCROLLDISTANCE));
        //一个开口向下,顶点(SCROLLDISTANCE,1),过(0,0),(2*SCROLLDISTANCE,0)的二次函数
        factorOfScale = MAX(0,-1/(SCROLLDISTANCE*SCROLLDISTANCE)*Y*(Y-2*SCROLLDISTANCE));

        CATransform3D t = CATransform3DIdentity;
        t.m34  = 1.0/-1000;
        t = CATransform3DRotate(t,factorOfAngle*(M_PI/5), transition.y>0?-1:1, 0, 0);
        t = CATransform3DScale(t, 1-factorOfScale*0.2, 1-factorOfScale*0.2, 0);

        currentPhoto.layer.transform = t;

解题完毕！

PS:这个动画出现在我最近写的一个图片浏览库 KYElegantPhotoGallery 中，你可以到这里查看这个优雅的图片展示控件。